GLKH
Version 1.1 (March 2021)
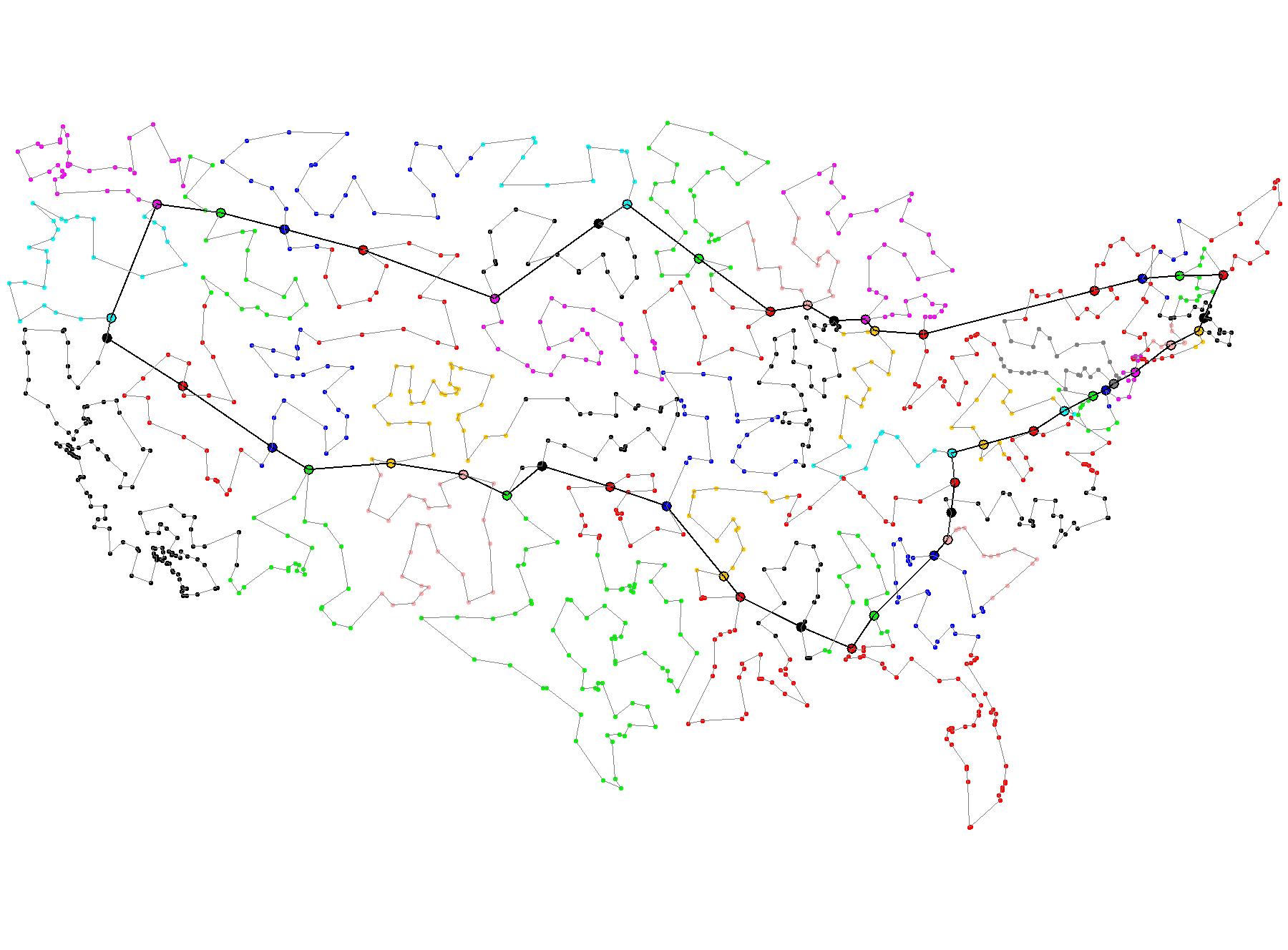
GLKH transforms an E-GTSP instance into an asymmetric TSP instance and solves the latter using the TSP-solver LKH. The E-GTSP solution is extracted from the obtained TSP solution. Despite that LKH is not modified in order to cater for the unusual structure of the TSP instances, GLKH's performance is quite impressive. All instances in a well-known library of E-GTSP benchmark instances, GTSPLIB, could be solved to optimality in a reasonable time, and it was possible to find high-quality solutions for a series of new large-scale E-GTSP instances with up to 17,180 clusters and 85,900 vertices.
GLKH has been described in the report
K. Helsgaun,
Solving the Equality Generalized Traveling Salesman Problem Using the Lin-Kernighan-Helsgaun Algorithm.
Computer Science Report #141, Roskilde University, 2014.
and in the paper
K. Helsgaun,
Solving the Equality Generalized Traveling Salesman Problem Using the Lin-Kernighan-Helsgaun Algorithm.
Mathematical Programming Computation, September 2015, Volume 7, Issue 3, pp 269-287.
Installation
GLKH has been implemented in the programming language C and runs under Unix/Linux.
Source code, test instances and solution tours can be downloaded here: GLKH-1.1.tgz (gzipped tar file, approximately 12 MB).
Execute the following UNIX commands:
tar xvfz GLKH-1.1.tgz
cd GLKH-1.1
make
Four executable files called GLKH, GLKH_EXP, GLKH_CHECK, and LKH will now be available in the directory GLKH-1.1.
GLKH is used for solving a given instance once, whereas GLKH_EXP is used for solving an instance using a specified number of independent runs.
GLKH_CHECK may be used to check that a solution tour is feasible (i.e., visits each cluster exactly one and has the correct length).
LKH is an executable of LKH-2.0.9.
To ease the running of GLKH and GLKH_EXP, two scripts, runGLKH and runGLKH_EXP, are provided. They create suitable parameter files and next execute GLKH and GLKH_EXP, respectively.
The scripts runSmall, runLarge and runVeryLarge can be used for solving the GTSPLIB instances. It is recommended to run the script runSmall in order to test the installation:
./runSmall
The software is distributed for research use. The author reserves all rights to the code.
BAF instances
In his PhD thesis, “Techniques hybrides de recherche exacte et approchée: application à des problèmes de transport” (2008), Boris Bontoux defined a series of GTSP instances, where the groups (clusters) are not formed by a clustering method (as is the case for GTSPLIB), but are formed pseudorandomly. The current best g-tour costs found by GLKH are reported here. The instances and the g-tours can be downloaded here in tgz format.
MOM instances
The paper "M. Mestria, L. S. Ochi, and S. de Lima Martins: GRASP with path relinking for the symmetric Euclidean clustered traveling salesman problem, Computers & Operations Research, Vol. 40, Issue 12, pp. 3218–3229 (2013)" provides a suite of test instances for the Euclidean CTSP. However, these instances can also be used for testing GTSP-solvers. The current best tour costs found by GLKH are reported here. The instances (in GTSPLIB format) and the tours can be downloaded here in tgz format.
GTSP+ instances
The paper "S. L. Smith and F. Imeson: GLNS: An Effective Large Neighborhood Search Heuristic for the Generalized Traveling Salesman Problem, Computers & Operations Research (2017), provides a library of GTSP instances by adding constraints to some GTSPLIB instances. The current best tour costs found by GLKH are reported here. The instances (in GTSPLIB format) and the tours can be downloaded here in tgz format.
A 115,475-city instance
Professor William J. Cook has proposed a 115,475-city challenge through (nearly) all cities, towns, and villages in the contiguous 48 states, plus the District of Columbia. A GTSP version of the challenge is provided here. The current best tour for this version was found by GLKH and has a length of 109,360.
Arc routing problem instances
Many arc routing problems can be transformed into E-GTSP. The report
K. Helsgaun,
Solving Arc Routing Problems Using the Lin-Kernighan-Helsgaun Algorithm.
Technical Report, Roskilde University, 2014.
evaluates the performance of GLKH on a broad class of transformed arc routing problems. It is shown that GLKH makes it possible to find solutions of good quality to large-scale undirected, mixed, and windy postman and general routing problem instances. The developed software is free of charge for academic and non-commercial use and can be downloaded here in source code together with test instances (45 MB).
CHANGES IN VERSION 1.1:
LKH-2.0.9 is used instead of LKH-2.0.7. This makes POPMUSIC candidate edge generation and GPX2 recombination available.
VERSION 1.0:
Created December 2013.